marktplatz

The everlasting need for a competent interviewer

An elementary component of Repertory Grid procedures is the web interface, which is used to conduct supervised interviews. The goal of these interviews is to accumulate expert opinions and store them in a database, so that these data can later be evaluated and visualized using clustering and other algorithms. The need for human accompaniment of these interviews is problematic in many respects, but in order to ensure a high quality of the collected data is indispensable. Besides a general introduction to the use of the interview tool, the control of the experts' free text input (construct evocation) is an essential part of the interviewers job. From these free text inputs, the clustering algorithms form opinion constructs, arrange them spatially and relate them to each other. Since these constructs are important for the algorithmic processing, the task of the interviewer is to pay attention to the quality of these constructs and, if necessary, to instruct the expert to enter qualitative constructs without influencing his opinion. Currently, interviews are conducted bilaterally, i.e. an interviewer interviews an expert.

Now it is time to automate qualitative interviews

Due to a higher number of interviews is required for an evaluation, the time for a development of an automated solution has come.

We are currently working on an implementation of a neural network based KI solution for our existing Repertory Grid Softwarepackage rep:bit. The neural network system biind the data base qualitatively evaluates constructs by means of machine learning and weights them according to specified quality criteria for algorithmic evaluation.

The developed software accesses a database of constructs entered in previous interviews, which were qualitatively evaluated by a trained interviewer on a scale from 0 (bad) to 1 (good) and annotated (e.g. "ambiguous construct term", "situational", "superficial", "meaningful", etc.). These annotations are standardized and are intended to provide feedback for the expert in productive use during interviews and tempt him to create the best possible constructs.

The database consists of approx. 1500 evaluated constructs and is to be used to teach a neural network that is to take over the evaluation and qualitative classification of the constructs. Since the data set used is relatively small, this database will be extended over time with the contructs of further interviews to increase the accuracy and correctness of the construct evaluations and thus the reliability of the predictions. The current amount of data sets allows only imprecise predictions, therefore the interviews will continue to be conducted bilaterally, but with the difference that the interviewer can rely on the evaluation of the constructs by the neural network (see Figure 1).

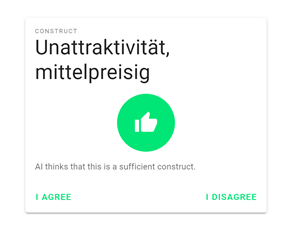Figure 1: Evaluation by the neural net during the input of a construct

These new features are supported by machine learning (ML) algorithm coming from the cooperation with the Sprachinstitut of the Informatic Faculty at the University of Leipzig (see also mindset project: https://mindset.wifa.uni-leipzig.de/)

If the evaluation of the neural network makes an incorrect prediction, the interviewer can correct it, keyword it and send it to the database to improve the learning model used. If the prediction is correct, the interviewer can mark the prediction as correct and send it to the database, so that this evaluation is weighted higher in the training of the neural network.

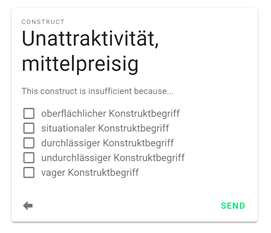Figure 2: Detection of an incorrect construct

How we approach the matter

Our current database consists of about 1500 evaluated constructs. These constructs are to be used for the training of a neural network, which is to take over the evaluation and qualitative classification of the constructs. Since the data set used is relatively small, this database will be extended over time with the constructs of further interviews to increase the accuracy and correctness of the construct evaluations and thus the reliability of the predictions.

The current amount of data sets allows only imprecise predictions, so the interviews will continue to be conducted bilaterally, but with the difference that the interviewer can rely on the neural network's evaluation of the constructs. If the evaluation of the neural network makes an incorrect prediction, the interviewer can correct it, keyword it and send it to the database to improve the learning model used. If the prediction is correct, the interviewer can mark it as correct and also send it to the database, so that this evaluation is weighted higher when training the neural network.

So far Python was used for the implementation of the arithmetic operations. Currently we are testing how the artificial neural networks based on multidimensional data fields can be executed with TensorFlow. In the course of the conversion to TensorFlow, a systematic component structure of the new software unit was created, which is structured as follows (see also Figure 3):

• The interview tool: Web interface for the input of constructs and the execution of interviews
• Construct DB: database for storing unrated and rated constructs
• Construct-Api: Interface for the administration of constructs and construct characteristics in the database
• ML-Api: Interface for mechanical supported evaluation of constructs GPU cluster: GPU-accelerated neural network

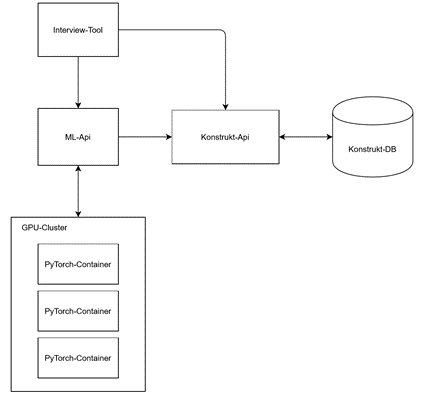Figure 3: Component structure of the software unit

How it has been realized so far

The interview tool is a web interface realized with Vue.js that is used to conduct interviews. During the interview, the expert is asked to characterize distinguishing features from which the personal constructs are derived.

While typing into the text field, using the HTTP client Axios, the content of the field is sent to the ML-Api, which, taking into account the already evaluated constructs, performs a qualitative classification of the input and replies with the result as a JSON response. The following code snippet shows the response of the ML-Api to a query with the construct "too little customer-oriented.

Figure 4: Code excerpt ML API from interview

Under "details" the implementation of the used machine learning algorithm is described (in this case a "classification" with the Python library "klearn" using the training model sof-b). The array results consists of the text of the construct (sentence), the quality of the construct (label), the probabilities for the corresponding construct quality (label_probabs) and the natural logarithm of the probabilities (logits). According to the response, the expert is shown in the web interface whether the construct is of good or bad quality.

ML-ApiH2 The ML-Api (Machine-Learning-Api) is an interface realized with the Python-Library Flask between the GPU cluster from MINDSET for machine-supported evaluation of constructs, the interview tool and the construct api. The MLApi can be used to initiate the training of the neural network. After modeling, constructs can be sent to the ML-Api for evaluation.

GPU-ClusterH2 The GPU cluster performs the GPU-accelerated calculation of the construction quality. The processes run on docker containers and use the machine learning framework PyTorch.

construct-ApiH2 The construct api is an interface for the management of evaluated and unevaluated constructs and for the management of quality criteria of constructs. The constructs can be filtered according to whether there is a user rating or a rating by the neural network and whether they differ. The following example shows a response of the api where the interviewer's assessment differs from the prediction of the neural network (see Figure 5).

Figure 5: Response API

The key "tags" contains the already mentioned remarks, which the interviewer has to give as reasons for his evaluation deviating from the neural network. The "ai_rating" contains the prediction of the neural network. The "user_rating" contains the rating of an interviewer of the construct women.

Construct DBH2 The construct DB is a MongoDB database for storing the constructs.

The Future

In the context of an evaluation project first experiences were made about the quality and reliability of the AI database. In the further course of the Mindset project further - at first German-language - libraries will be added to train all new text units (constructs) and to determine additional modules for normalization, toenization and segmentation.